Данная работа посвящена некоторым вопросам о свойствах нормы в нормированных пространствах измеримых функций и является продолжением выпускной работы автора на степень бакалавра.
Приведены условия (A) (порядковая непрерывность нормы), (B) (монотонная полнота нормы), (C) (порядковая полунепрерывность нормы), которыми норма в нормированном идеальном пространстве (НИП) измеримых функций может обладать, а может не обладать. Суть этих условий навеяна утверждениями из теорем Леви, Фату, Лебега о предельном переходе под знаком интеграла. Здесь же приведены примеры пространств, демонстрирующих, что эти условия независимы друг от друга.
В статье рассматриваются условия (Cλ), (C∗), более слабые, чем условие (C). Здесь также получена связь между условиями (Cλ) при различных λ и приведён пример НИП, в котором не выполняется условие (C∗).
Приведены и доказаны утверждения, что условие (D) и диагональное условие (D2) эквивалентны условию (B) (свойство Фату монотонной полноты нормы).
Предварительные сведения и терминология
В терминологии и обозначениях из теории нормированных пространств измеримых функций мы будем придерживаться терминологии и обозначений, принятых в монографии [1].
Пусть (T,Σ,μ) — пространство с мерой. Здесь T — множество; Σ — σ-алгебра его подмножеств; μ — полная σ-конечная мера на Σ (σ-конечность меры означает, что существует представление 
такое, что 
, а полнота μ означает, что A ⊂ B ∈ Σ, μ(B) = 0 следует A ∈ Σ и, следовательно, μ(A) = 0).
Через S = S(T, Σ, μ) обозначается множество всех, почти всюду (п.в.) конечных измеримых функций на T. Эквивалентные функции, то есть совпадающие почти всюду на T , будем отождествлять. Если x ∈ S (x — класс эквивалентных между собой функций), то через x(t) будем обозначать любую функцию из класса x, причём можно считать, что x(t) конечна для любого t.
Элементы x,y ∈ S называются дизъюнктными (обозначение: xdy), если x(t)·y(t) = 0 п.в. Для последовательности xn ∈ X (n = 1, 2, . . .) по определению полагают (sup xn)(t) = sup xn(t), t ∈ T . n
В S можно ввести частичный порядок, полагая для x,y ∈ S, по определению x ⩽ y, если x(t) ⩽ y(t) п.в.
Пусть xn,x ∈ S(1, 2, . . .). Говорят, что:
1) xn возрастает (xn ↑), если xn+1 ⩾ xn, ∀n;
2) xn возрастает вбок (xn ↑_), если xn ↑ и (xn+1 − xn)dxn;
3) xn возрастает к x (xn ↑ x), если xn ↑ и xn(t) → x(t) п.в.;
4) xn возрастает вбок к x (xn ↑_ x), если xn возрастает вбок и xn ↑ x.
Аналогично определяются последовательности {xn} убывающие (xn ↓), убывающие вбок (xn ↓_), убывающие к x (xn ↓ x), убывающие вбок к x (xn ↓_ x)
Для x ∈ S модуль |x| определяется по формуле: |x|(t) = |x(t)|.
Идеальным пространством (ИП) на (T,Σ,μ) называется подмножество X ⊂ S, такое, что:
1) X — линейно (x, y ∈ X → αx + βy ∈ X);
2)(x∈X, y∈S, |y|⩽|x|)⇒y∈X.
Возрастающая последовательность 
в ИП X называется порядково ограниченной сверху в X (ограниченной по упорядочению), если ∃y ∈ X, такой, что x ≤ y для всех n ∈ N. Если возрастающая последовательность не ограченна в X, то пишут xn ↑ +∞. Норма ||·|| на ИП X называется монотонной, если ∀x, y ∈ X, |x| ⩽ |y|⇒||x|| ⩽ ||y||. В частности, |||x||| = |x|. Нормированным идеальным пространством (НИП) на (T,Σ,μ) называется ИП, снабжённое монотонной нормой. Полное по норме НИП называется банаховым идеальным пространством (БИП).
Хорошо известны следующие классические теоремы из математического анализа о предельном переходе под знаком интеграла Лебега (см., например, [1]).
Теорема 1 (Леви) Если xn ∈S, xn(t)⩾0 и xn ↑x, то
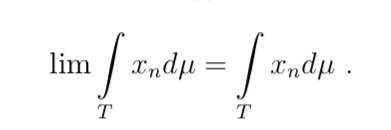
Теорема 2 (Фату) Если xn ∈ S, x(t) ⩾ 0 и xn(t) → x(t) п.в., то
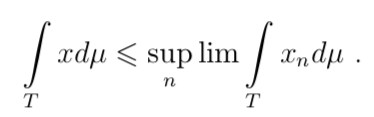
Теорема 3 (Лебег) Пусть
1) xn(t) → x(t) п.в. на T;
2) ∃ суммируемая функция y такая, что |xn(t)| ⩽ y(y) п.в. Тогда x — суммируема и
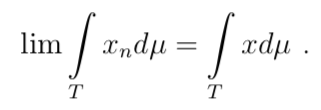
Порядковые свойства нормы
Монотонная норма в НИП может обладать различными порядковыми свойствами (см., например, [1], [2], [3]).
Следующие три условия, налагаемые на произвольную норму в НИП X, являются перефразировкой вышеуказанных теорем Леви, Фату и Лебега с формальной заменой интеграла (норма в пространстве L1) нормой в X.
Пусть (X, ||·||) — НИП на (T, Σ, μ). Говорят, что
1) норма в X (порядково) непрерывна, если выполнено условие (A): из X∋xn ↓0 следует ||xn||→0;
2) норма в X (порядково) монотонна полна, если выполнено условие (B): 0⩽xn ↑, xn ∈X, sup||xn||n ∈X;
3) норма в X (порядково) полунепрерывна, если выполнено условие (C): 0⩽xn ↑x∈X ⇒lim||xn||=||x||.
Ясно, что (A)⇒(C) (обратное неверное (см. пример 4)). Действительно, если xn↑x, то x−xn ↓ 0 в силу (A): ||xn−x||→0,а так как ||xn||⩾ ||x|| − ||x − xn||, то lim ||xn|| ⩾ ||x||. Обратное неравенство lim ||xn|| ⩽ ||x|| следует из монотонности ||xn|| ⩽ ||x||. Как показывают следующие примеры, других связей между этими порядковыми свойствами, вообще говоря, нет.
Примеры
1. Из теорем Леви, Лебега и Фату о предельном переходе под знаком интеграла следует, что в пространстве L1(T) с обычной нормой 
выполнены все условия (A), (B), (C).
2. Простраство c0 с обычной нормой удовлетворяет условию (A) и не удовлетворяет условию (B). Действительно, пусть 0 ⩽ xn ∈ c0; xn ↓ 0. Если 
,причём для 
. Пусть ε > 0. Далее 
. Существует k0 такое, что 
при k>k0. Тогда при k>k0 и любом n. Так как 
при n ↑ ∞ и k = 1,2,...,k0 , то ∃n0 такое, что все 
. Тогда при 
, то есть lim||xn||=0.
3. Приведём пример пространства со свойством (B) и без свойства (C).
Рассмотрим пространство l∞. Для 
полагаем 
В l∞ можно рассмотреть и обычную норму ||x||∞ = sup|ak|, а так как ||x||∞ ⩽ ||x|| ⩽ 2||x||∞, то эти две нормы эквиваленты и так как ||·||∞ очевидно удовлетворяет свойству (B), то и рассматриваемая норма ||·|| также обладает свойством (B). Положим xn = (1,...,1,0,...), x = (1,...,1,1,...). Тогда 0⩽xn↑x, ||xn||=1, а ||x||=2,то есть lim||xn||≠||x|| или в X не выполнено свойство (C).
4. Пространство c0 с обычной нормой удовлетворяет условию (B) и (C) и не удовлетворяет условию (A). Действительно, пусть xn = (0, . . . , 0, 1, . . .), xn↓ = (0,0,...,0)=0,но 
,то есть в X нет (A).Тогда 
(то есть 
) при n→∞. И ||x||⩽C, 
Если заменим во всех трёх условиях (A), (B), (C) монотонные последовательности последовательностями монотонными вбок, то получим формально более слабые условия (Ad), (Bd), (Cd). Однако (см. [1]) эти условия эквиваленты: (A) ⇔ (Ad), (B) ⇔ (Bd), (C) ⇔ (Cd).
Другие специальные порядковые свойства нормы в НИП
Пусть число λ⩾1. Говорят, чтоX∈(Cλ), если из 0⩽xn↑x∈X следует ∥x∥ ⩽ λlim||xn||. Ясно, что если λ < μ и X ∈ (Cλ), то X ∈ (Cμ). Покажем, что обратное неверно.
Пример 1
Пусть 1⩽λ∞ по составу элементов и для 
Покажем, что 
. Положим
Тогда ||xn||=1 и xn ↑x=(1,...,1,1,...)=x, а ||x||=μ>λlim||xn|| и, следовательно, .
Проверим, что X ∈ (Cμ). Пусть 
, а x = (a1,a2,...,ak,...). Тогда xn↑x и для любого k получаем, 
.
Тогда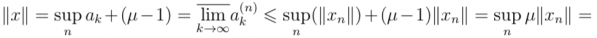 
.
Говорят, что в X выполнено условие (C∗) (X ∈ C∗), если ∃λ ⩾ 1 такое, что x ∈ (Cλ).
Пример 2
Здесь мы приведём пример НИП (X, ||·||), в котором не выполнено условие (C∗). Пусть k — натуральное число. Рассмотрим Xk = l∞ по составу и для x ∈ Xk ||x||k = sup |ak| + klim|ak|. Тогда 
, так как если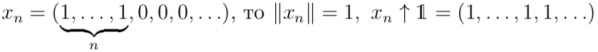 
Строим пространство X по типу l∞ , точнее 
, где все Xk = l∞ по составу. Элементы этого пространства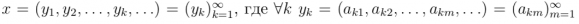 
т.ч. 
Итак, 
— матрица, т.ч. 
Достаточно показать, что 
для любого натурального N. Пусть xn =(akn),где akn=1 при1⩽k⩽n, 1⩽m⩽N+1, остальные akn =0
Тогда xn ↑x=(bkm),где bkm=1 при 1⩽kkm= 0
Тогда легко видеть, что ||xn||=1, а ||x|| = N + 1. Поэтому .
Как уже указано ранее, условия (B) и (C) независимы друг от друга. И, например, из условия (B) не следует условие (C). Однако, как показывает следующее утверждение, из условия (B) следует формально более слабое условие (C∗), т.е. при выполнении условия (B) выполняется условие (Cλ) при некотором λ ⩾ 1.
Теорема 4 Если X ∈ (B), то X ∈ (C∗).
Доказательство. Пусть это не так, т.е. 
для любого X. Так как 2n ·m не является числом λ, то 
и 
. Положим yn =x1n +x2n +...+xnn. Тогда
yn+1 = x1,n+1 +x2,n+1 +...+xn,n+1 +xn+1,n=1, то есть 0 ⩽ yn ↑ и
По (B) ∃z∈X т.ч. yn⩽z, ∀n. Если m фиксированно, то xmn⩽yn⩽z, и поэтому am⩽z, то есть m⩽||z|| для всех натуральных чисел m.
О свойстве монотонной полноты нормы в НИП
В этом пункте мы приведём два свойства в НИП X, которые эквивалент- ны условию (B) — свойству монотонной полноты нормы.
Говорят, что НИП X удовлетворяет условию (D) (X ∈ (D)), если для любой последовательности xn такой, что
0⩽xn↑∞, существует такая числовая последовательность ξn↓0, что 
не ограничена в X по упорядочению.
Будем говорить, что НИП X удовлетворяет условию (D2) (X ∈ (D2)), если из того, что 
для любого n следует что существует такая последовательность индексов mn (n = 1, . . .) такая, что 
не ограничена по упорядочению в X.
Лемма 1 Пусть X — НИП. Тогда, если X ∈(D2), то X ∈(D). Действительно, пусть 0 ⩽ xn ↑ +∞. Положим 
, (m,n= 1,2,...). Тогда 
для любого n. Так как x ∈ (D2), существует 
, что 
не ограничена в X, то есть 
не ограничена. Положим,
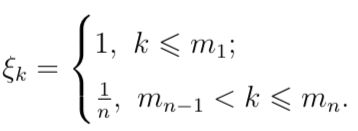
Нетрудно видеть, что последовательность mn возрастающая. Ясно, что тогда 
не ограничена в X.
Теорема 5 Для любого пространства X (БИП) следующие утверждения эквивалентны:
1) в X выполнено (B),
2) в X выполнено (D),
3) в X выполнено (D2).
Проведём доказательство про схеме (3) ⇒ (2) ⇒ (1) ⇒ (3). Импликация (3) ⇒ (2) доказана в лемме 1. Докажем импликацию (2) ⇒ (1): достаточно убедиться, что в X выполнено (Bd). Допустим противное, то есть существует последовательность 0 ⩽ xn ↑_ и sup||xn||< +∞. Допустим, что sup xn = +∞ в X по умолчанию. Положим, y1 = x1; yk = xk − xk−1. Тогда yidyi (i ≠ j). Рассмотрим ряд:
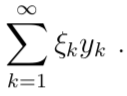
Тогда при m < n имеем 
Поэтому 
сходится по мере (т.к. X — банахово). Пусть 
(сходимость ряда по норме). Тогда: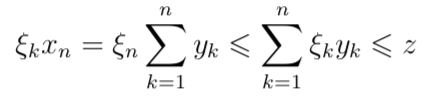 
для любого n, то есть ξnxn ограничена по упорядочению.
Наконец, докажем импликацию (1) ⇒ (3): пусть 
для любого n. В силу (B) справедливо 
для любого n. За mn берём такой индекс, что 
. А тогда 
не ограничена по упорядочению, так как не ограничена по норме, то есть в X выполнено (D2).
Список литературы
[1] Л. В. Канторович, Г. П. Акилов. Функциональный анализ / М.: Наука. Изд. 3-е, 2004 - с. 752
[2] П. П. Забрейко. Идеальные пространства функций / Вестник Ярославского университета, 2003., Выпуск 8, с. 12—52
[3] W. A. J. Luxemburg, A. C. Zaanen. Riesz spaces. Vol. I. North-Holland Mathematical Library. North-Holland Publishing Co., Amsterdam — London; Americam Elsevier Publishing Co., New York, 2005, p, 521
[4] Т. А. Самусенко. Порядковые свойства нормы в пространствах измеримых функций. Выпускная квалификационная работа, 2015