Изучение поведения реальной электроэнергетической системы (далее ЭЭС), в частности, электромеханических переходных процессов, происходящих после различных возмущений, требует создания динамической модели этой энергосистемы. Оценка достоверности модели происходит в результате валидации – проверки точности соответствия изменения режимных параметров во времени компьютерной модели и реальной ЭЭС. Валидация является одной из важнейших задач в электроэнергетике, так как динамическая модель, поведение которой идентично поведению реальной энергосистемы, позволяет достоверно оценивать последствия аварийных событий и принимать превентивные меры для нивелирования их последствий.
Исторически сложилось, что вместо термина «валидация» используется близкий по смыслу термин «верификация», который подразумевает под собой проверку на соответствие концептуальной модели и исправление различных ошибок ее функционирования. Так или иначе, второй термин получил большее распространение в области отечественной электроэнергетики, сохраняя смысл сравнения выходных данных модели с экспериментальными данными реальной энергосистемы. В связи с этим допустимо принять оба термина равнозначными. Данное допущение также обосновывается тем, что в ряде работ зарубежных авторов термины «верификация» и «валидация» используются для обозначения одного и того же, а именно проверки объекта компьютерного моделирования с тестовыми данными реального объекта физического мира. В частности, в работе Ричарда Дорлинга [Dorling: 3] эти термины являются взаимозаменяемыми.
Проблема валидации динамической расчетной модели (далее ДРМ) рассматривается в кандидатской диссертации А.Н. Смирнова [Смирнов: 2]. В частности, в этой работе особое внимание уделяется анализу принципов оценки адекватности моделей, а также разработке технологии актуализации и верификации ДРМ, которая включает в себя принципы и методы верификации, критерии и количественные показатели качества, развитие методов настройки ДРМ.
Одной из программ, которая позволяет как создавать, так и верифицировать динамические модели ЭЭС, является «Dymola» (сокр. от «Dynamic Modeling Laboratory» – лаборатория динамического моделирования). Программа «Dymola» представляет собой коммерческую среду для моделирования на основе открытого языка Modelica, которая позволяет создавать динамические модели авиационных, термодинамических, химических, электрических и прочих систем, имеет обширный функционал для создания графического интерфейса динамической модели, оптимизации параметров, постобработки, выгрузки результатов моделирования в различные форматы и т. д.
Использование языка программирования Modelica для описания переходных процессов в области электроэнергетики и электротехники подробно рассмотрено в работе А.Н. Беляева [Беляев: 3]. На основании подходов и принципов моделирования элементов ДРМ энергосистемы, представленных в данной работе, была составлена модель реального энергообъединения в ПК «Dymola».
Целью данной работы является сравнение различных методов валидации с использованием программного комплекса (далее ПК) «Dymola» – как простейших, связанных с последовательным изменением параметров модели на основании их известного влияния на переходные процессы, так и более сложных, связанных с итерационными функциями данного ПК. При этом решаются следующие задачи:
- создание модели части объединенной энергосистемы (далее ОЭС) Северо-Запада;
- сравнение кривых переходных процессов, возникающих в результате реального аварийного возмущения в Кольской энергосистеме.
В работе применяются положения методологии комплексного оценивания качества объектов. В работе использованы методы компьютерного моделирования в ПК «Dymola», программирования на основе языка Modelica, сопоставления различных методов валидации динамической модели.
* * * * *
В целом, процесс валидации основывается на экспертной оценке изменения во времени выбранных параметров электрического режима, который можно назвать методом визуального сравнения. На основании сравнения графиков имевшего место в реальной энергосистеме переходного процесса и полученного в результате моделирования принимается решение об изменении тех параметров, которые могут увеличить степень соответствия описанных графиков.
В качестве примера рассмотрим механическую инерционную постоянную времени Tj i-го генератора. Данный параметр фигурирует в уравнении движения ротора:
Tj*`(ds)/(dt)` = Mт - Me (1)
где Mт – механический момент на валу генерирующего агрегата;
Me – электромагнитный момент;
s – скольжение ротора генератора;
t – время.
Исходя из представленных уравнений, при одинаковом небалансе моментов, приложенных к валу генерирующего агрегата машина с большим значением Tj будет испытывать меньшее изменение скольжения за единицу времени (другими словами, будет испытывать меньшее по модулю угловое ускорение), и наоборот.
Рассмотрим пример реального возмущения в энергосистеме операционной зоны Ленинградского регионального диспетчерского управления (далее РДУ). В результате короткого замыкания (далее – КЗ) на отходящей от шин высокого напряжения электростанции воздушной линии (далее ВЛ) 110 кВ № 1 произошло отключение этой линии действием релейной защиты. На рисунке 1 приведены графики зависимости активной мощности ВЛ 110 кВ № 2 при увеличении Tj генераторов данной станции. Синим цветом обозначена кривая активной мощности по данным регистратора аварийных событий (далее РАС), а красным – полученная в динамической модели.
а) 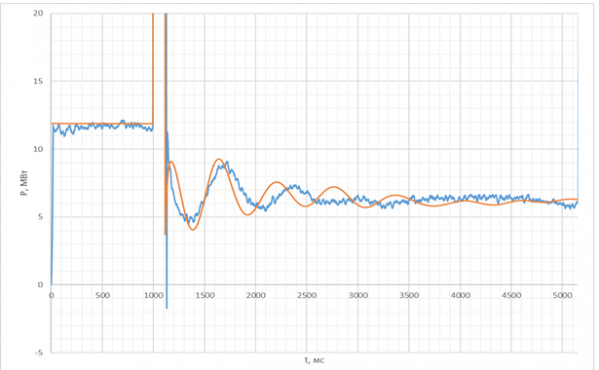
б) 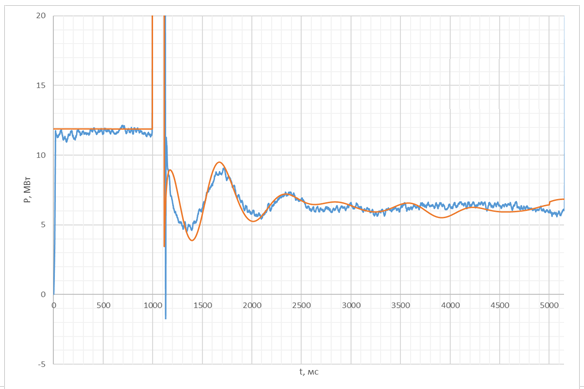
Рис. 1. Электрическая активная мощность ВЛ 110 кВ, отходящей от шин станции при увеличении Tj её генераторов: а) 6 с; б) 8,631 с. Здесь и далее составлено автором
Как видно из рисунков выше, при увеличении Tj удалось добиться соответствия частоты колебаний, что полностью согласуется с формулой (1): большему значению Tj соответствует меньшая частота колебаний.
Другим примером является изменение параметров форсировки возбуждения генератора. Помимо кратности форсировки по току и напряжению, работу форсировки определяют такие параметры, как:
– напряжение ввода форсировки Uвв_форс;
– напряжение снятия форсировки Uсн_форс;
– задержка времени после снятия форсировки Tз_снятия.
Во время форсировки происходит увеличение напряжения возбуждения сверх своего номинального значения, что способствует повышению динамической устойчивости. На рисунке 2 приведены графики напряжения на шинах станции при снижении напряжения ввода форсировки. Синим цветом обозначена кривая напряжения по данным РАС, а красным – полученная в динамической модели.
а) 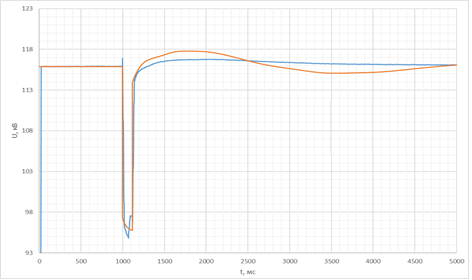
б) 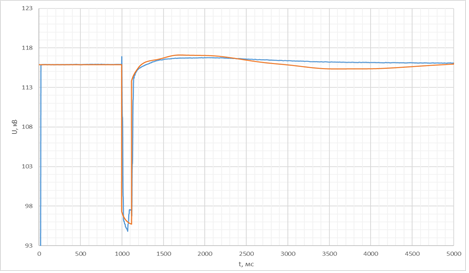
Рис. 2. Напряжение прямой последовательности шин станции при уменьшении Uвв_форс её генераторов: а) 0,85; б) 0,8
Как видно из рисунков выше, при уменьшении Uвв_форс удалось добиться большего соответствия колебаний напряжения, поскольку во втором случае форсировка не вводится в работу.
По аналогии проводится изменение других параметров динамической модели.
Метод ручного изменения параметров удобен в том случае, если верифицируемый параметр модели имеет конечное число стандартизированных значений (например, задержка времени на снятие форсировки может принимать только типовые значения 0, 0.1 или 0.2), большая часть модели уже верифицирована, и изменению может быть подвержено лишь конечное число параметров, известны уравнения и четкие физические законы, которые позволяют однозначно предсказать, каким образом изменение выбранного параметра будет влиять на переходный процесс.
Для учета одновременного влияния двух параметров на переходный процесс возможно использование встроенной функции «sweep parameters», которая относится к библиотеке «Experimentation» и включает в себя производные функции: «sweepOneParameter», «MonteCarloAnalysis», «sweepManyParameters» и «sweepManyParametersTrajectory»1. Данные функции позволяют:
- строить графики анализируемой переменной при варьировании одного параметра;
- анализировать случайный выбор чисел при моделировании методом Монте-Карло с возможностью построения точечных диаграмм;
- варьировать несколько параметров с выводом значений переменной в последней точке расчетного интервала;
- варьировать несколько переменных с выводом графика переменной на всем расчетном интервале.
Рассмотрим пример реального возмущения в энергосистеме операционной зоны Кольского РДУ. В результате КЗ на второй цепи ВЛ 330 кВ произошло отключение этой цепи действием релейной защиты. Анализируется изменение активной мощности по первой цепи этой же линии (в модели обозначена как L0709_1) по данным системы мониторинга переходных режимов (далее СМПР).
В рамках метода попарного перебора параметров оценивается изменение графика анализируемой переменной при одновременном изменении двух параметров модели. Рассматривается поочередное изменение коэффициентов регулирования по отклонению и производной отклонения частоты Koω и K1ω автоматического регулятора возбуждения (далее АРВ) эквивалентного генератора электростанции, расположенной наиболее близко к точке КЗ – в модели обозначен как G07. Диапазон изменения для предварительного расчета: от -5 до 5 с шагом в 2 о. е. Выбранное значение шага изменения Koω и K1ω является оптимальным для соответствующего диапазона как с точки зрения скорости расчета, так и с точки зрения количества выводимых графиков, представленных на рисунке 3.
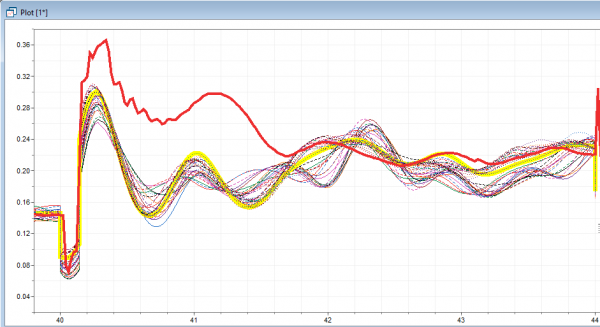
Рис. 3. Визуальная оценка кривой активной мощности L0709_1, которая в наибольшей степени соответствует данным СМПР
Путем поочередного выделения кривых в Dymola (желтая кривая на рисунке 3), удалось выявить предварительные значения коэффициентов, при которых визуальное совпадение двух кривых оказалось наибольшим:
Koω = -5 и K1ω = 1.
Для дальнейшего уточнения значений двух выбранных параметров был выбран диапазон [-6;-4] для Koω и [0;2] для K1ω с шагом 0,25 и произведен повторный расчет. Путем аналогичного поочередного выделения кривых удалось выявить уточненные значения наиболее оптимальных параметров, которые составили Koω и K1ω –4 и 2 соответственно.
Функция sweep parameters позволяет также получать зависимость значения выбранной переменной в конкретный момент времени от изменения двух произвольных параметров. В контексте рассматриваемого примера эта функция может быть полезной для достижения соответствия данным СМПР величины провала напряжения в точке КЗ, соответствующей шинам высокого напряжения G07, которая составляет 0,46276 о.е. При варьировании значений активной и реактивной проводимости шунта КЗ Gn и Bn соответственно было получено распределение значений напряжения в точке КЗ в момент начала аварийного возмущения, что представлено на рисунке 4.
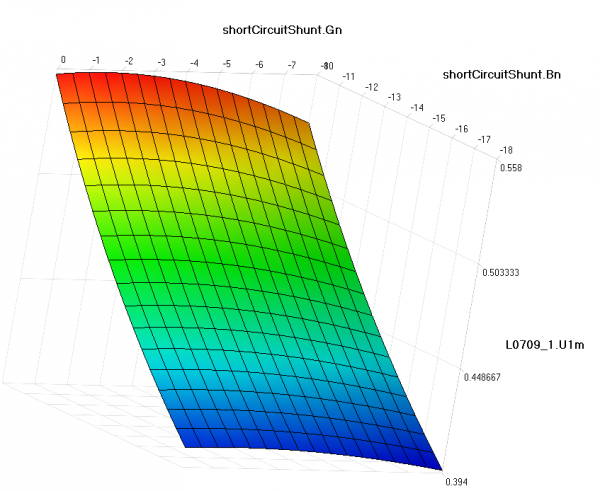
Рис. 4. Зависимость напряжения в узле № 7 при одновременном изменении активной и реактивной проводимостей шунта КЗ
Из рисунка 4 видно, что значению 0,46276 соответствует некоторое множество пар значений Bn и Gn. При подстановке, например, значений Bn = ‑14, а Gn = -4, получим, что величина провала напряжения по данным СМПР и в ПК Dymola совпадают, что представлено на рисунке 5.
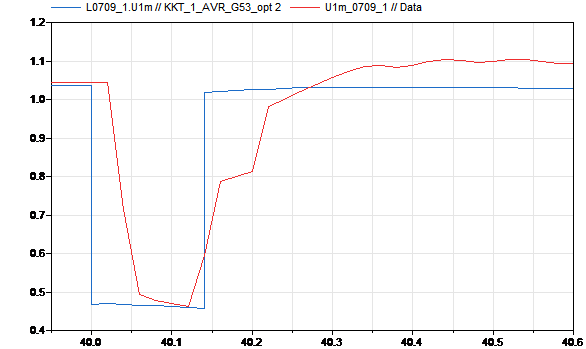
Рис. 5. Напряжение в узле № 7 после начала КЗ по данным СМПР (синяя кривая) и Dymola (красная кривая)
Несмотря на то, что это лишь одна из пар множества значений активной и реактивной проводимости, этого достаточно, чтобы определить величину модуля полной проводимости шунта КЗ:
Z n = `sqrt(Bn^(2)+Gn^(2)) ` (2)
Теперь при сохранении неизменным величины Zn допустимо менять соотношение между Bn и Gn, которое оказывает влияние на дальнейший переходный процесс.
Метод попарного перебора параметров удобен в том случае, если требуется найти оптимальное соотношение двух параметров, одновременное изменение которых оказывает труднопредсказуемое влияние на переходный процесс и которые могут принимать непрерывное множество значений в определенном диапазоне.
Одной из поставляемых вместе с программой Dymola является библиотека «Design», которая предназначена для оптимизации моделей. Одной из функций библиотеки является калибровка параметров модели («calibration»)2. Метод оптимизации, используемый этой функцией, заключается в изменении определенных настраиваемых параметров в задаваемом пользователем диапазоне по методу наименьших квадратов. При этом используется регуляризация – введение дополнительных ограничений, которые предотвращают «переобучение системы». Несмотря на достаточно подробное описание использования функции3, её алгоритм, как отмечается в [Andersson: 4], недоступен пользователю, так как функция относится к защищенному программному обеспечению, что ограничивает её применение в исследовательских целях. В связи с этим авторы данной работы используют альтернативный алгоритм калибровки, основанный на оптимизации без использования производных. Данный алгоритм подробно описан в [Gedda: 5].
Перед началом калибровки используется функция валидации (validation), которая автоматически строит графики сравниваемых переменных с исходными значениями настраиваемых параметров. Стоит отметить, что даже при задании в команде «validation» времени начала расчета, близкого ко времени аварийного возмущения (например, 39,9 с), старт расчета в Dymola начинается с нулевых начальных условий. В результате на качания активной мощности, возникающие после короткого замыкания в начале линии, накладываются качания при установлении режима, в результате чего рассматривается совсем не тот переходный процесс, который планируется исследовать. В связи с этим для корректной работы описанных выше функций важно сохранить значения конечных доаварийных значений переменных состояния («continuous time states») в качестве начальных условий в модели. Графики, полученные в результате выполнения команды «validation», представлены на рисунке 6.
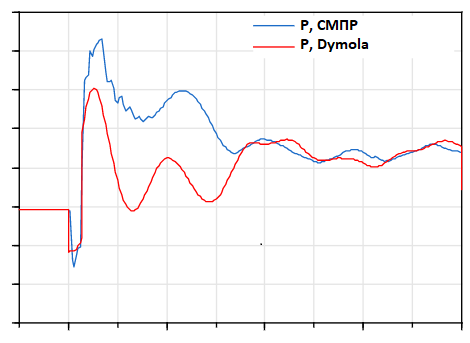
Рис. 6. Сравнение зависимости активной мощности L0709_1 по данным СМПР и модели Dymola до калибровки параметров
Перед началом выполнения калибровки модели необходимо определить состав и диапазон изменения настраиваемых параметров. Поскольку КЗ моделируется в узле, непосредственно к которому присоединен генератор G07, то логичным будет изменение параметров именного этого генератора. Опытным путем было определено, что даже значительное изменение параметров других генераторов, эквивалентирующих реальные электростанции Кольской энергосистемы, практически не оказывает влияния на переходный процесс.
Также калибровке подлежат параметры генератора, эквивалентирующего энергосистему, внешнюю по отношению к Кольской и Карельской – G01, который по сути представляет собой шины бесконечной мощности (далее ШБМ), поскольку её параметры задаются приближенно по оценочному значению мощности КЗ.
Несмотря на то, что данные сопротивлений и эквивалентных постоянных времени синхронных машин (далее – СМ), используемые в модели, соответствуют тем, которые были предоставлены собственниками соответствующих генерирующих объектов, эти параметры используются в процессе калибровки и изменяются в диапазоне +-30% от исходного значения по следующим причинам:
– погрешность приборов во время проведения испытаний, изменение физических свойств машин с течением времени, неучет параметров электромашинных систем возбуждения приводит к тому, что реальные значения сопротивлений синхронной машины могут отличаться от данных, предоставленных собственником;
– для уменьшения размерности динамической модели каждая электростанция представлена в виде эквивалентного генератора, который через эквивалентный же повышающий трансформатор присоединен к шинам веского напряжения, в то время как в реальности каждый генератор (максимум, пара генераторов) имеет свой собственный повышающий трансформатор. Данное упрощение вносит определенное искажение в динамическую модель, что позволяет варьировать сопротивления СМ в разумных пределах.
Варьирование коэффициентов регулирования АРВ может быть более широким. Это связано с тем, что персонал станции обладает определенной свободой действий в части настроек систем АРВ. Чтобы получить реальные значения параметров АРВ, необходимо регулярно получать листинг этих параметров, что в настоящее время не представляется возможным в виду технических и организационных ограничений. Полный список настраиваемых параметров приведен в таблице 1.
Таблица 1
Полный список настраиваемых параметров G01 и G07
| № | Обозначение | Наименование | Исходное значение | Минимум | Максимум | Итоговое значение |
| 1 | G07.xd_p | Синхронное реактивное сопротивление в продольной оси | 1,314 | 0,92 | 1,708 | 1,314 |
| 2 | G07.Xq_p | Синхронное реактивное сопротивление в поперечной оси | 1,314 | 0,92 | 1,708 | 1,315 |
| 3 | G07.Xs_p | Реактивное сопротивление рассеяния | 0,0820 | 0.0574 | 0,107 | 0,0781 |
| 4 | G07.X1d_p | Переходное реактивное сопротивление в продольной оси | 0,166 | 0,116 | 0,216 | 0,154 |
| 5 | G07.X2d_p | Сверхпереходное реактивное сопротивление в продольной оси | 0,110 | 0,0770 | 0,143 | 0,104 |
| 6 | G07.X2q_p | Сверхпереходное реактивное сопротивление в поперечной оси | 0,110 | 0,0770 | 0,143 | 0,127 |
| 7 | G07.Rf_p | Активное сопротивление обмотки возбуждения | 0,000601 | 0,000421 | 0,000781 | 0,000424 |
| 8 | G07.R1d_p | Активное сопротивление продольного демпферного контура | 0,000226 | 0,000159 | 0,000294 | 0,000158 |
| 9 | G07.R1q_p | Активное сопротивление поперечного демпферного контура | 0,000240 | 0,000168 | 0,000312 | 0,000163 |
| 10 | G07.Tj_p | Инерционная постоянная времени | 19,712 | 13,798 | 25,626 | 19,712 |
| 11 | G07.Kemax | Кратность форсировки по напряжению | 2,500 | 1,500 | 3.000 | 2,501 |
| 12 | G07.Kemin | Кратность расфорсировки по напряжению | -1,000 | -1,000 | 0,000 | -0,60168 |
| 13 | G07.K0u | Коэффициент регулирования по отклонению напряжения | -25,000 | -100,000 | 0,000 | -24,999993 |
| 14 | G07.K1u | Коэффициент регулирования по производной напряжения | -1,000 | -10,000 | 0,000 | -1,000 |
| 15 | G07.K0w | Коэффициент регулирования по отклонению частоты | -2,000 | -5,000 | 5,000 | -2,000 |
| 16 | G07.K1w | Коэффициент регулирования по производной частоты | 2,000 | -5,000 | 5,000 | 2,000 |
| 17 | G07.K1if | Коэффициент регулирования по производной тока ротора | 0,000 | -5,000 | 5,000 | 6,068 |
| 18 | G07.Uforc | Напряжение ввода форсировки | 0,850 | 0,750 | 0,900 | 0,850 |
| 19 | G07.Udeforc | Напряжение снятия форсировки | 0,950 | 0,900 | 1,000 | 0,950 |
| 20 | G07.Tforcedelay | Задержка снятия форсировки | 0.100 | 0,000 | 0,200 | 0,100 |
| 21 | G01.xd_p | Синхронное реактивное сопротивление в продольной оси | 0,041 | 0,0287 | 0,0533 | 0,0492 |
| 22 | G01.Xq_p | Синхронное реактивное сопротивление в поперечной оси | 0,041 | 0,0287 | 0,0533 | 0,0287 |
| 23 | G01.Xs_p | Реактивное сопротивление рассеяния | 0,00360 | 0,00252 | 0,00468 | 0,00468 |
| 24 | G01.X1d_p | Переходное реактивное сопротивление в продольной оси | 0,00550 | 0.00385 | 0,00715 | 0,00659 |
| 25 | G01.X2d_p | Сверхпереходное реактивное сопротивление в продольной оси | 0,0039 | 0,00273 | 0,00507 | 0,00273 |
| 26 | G01.X2q_p | Сверхпереходное реактивное сопротивление в поперечной оси | 0,0039 | 0,00273 | 0,00507 | 0,00273 |
| 27 | G01.Rf_p | Активное сопротивление обмотки возбуждения | 0,000601 | 0,0004207 | 0,0007813 | 0,00078 |
| 28 | G01.R1d_p | Активное сопротивление продольного демпферного контура | 0,000226 | 0,0001582 | 0,0002938 | 0,0001582 |
| 29 | G01.R1q_p | Активное сопротивление поперечного демпферного контура | 0,00024 | 0,000168 | 0,000312 | 0,000168 |
| 30 | G01.Tj_p | Инерционная постоянная времени | 378,88 | 265,216 | 492,544 | 378,880 |
| 31 | G01.Kemax | Кратность форсировки по напряжению | 2,000 | 1,500 | 3,000 | 2,000 |
| 32 | G01.Kemin | Кратность расфорсировки по напряжению | -0,600 | -1,000 | 0,000 | -0,600 |
| 33 | G01.K0u | Коэффициент регулирования по отклонению напряжения | -25,000 | -100,000 | 0,000 | -25,000 |
| 34 | G01.K1u | Коэффициент регулирования по производной напряжения | 0,000 | -10,000 | 0,000 | 0,000 |
| 35 | G01.K0w | Коэффициент регулирования по отклонению частоты | 0,000 | -5,000 | 5,000 | 0,000930 |
| 36 | G01.K1w | Коэффициент регулирования по производной частоты | 0,000 | -5,000 | 5,000 | 0,00209 |
| 37 | G01.K1i | Коэффициент регулирования по производной тока ротора | 0,000 | -5,000 | 5,000 | 0,0137 |
| 38 | G01.Uforc | Напряжение ввода форсировки | 0,850 | 0,750 | 0,900 | 0,850 |
| 39 | G01.Udeforc | Напряжение снятия форсировки | 0,900 | 0,900 | 1,000 | 0,900 |
| 40 | G01.Tforcedelay | Задержка снятия форсировки | 0,000 | 0,000 | 0,200 | 0,000 |
Cтоит отметить, что итоговые значения параметров после выполнения калибровки в программе имеют точность до 20 знаков после запятой. Это связано с тем, что функция калибровки может применяться к различным физическим системам, задание параметров которых может потребовать прецизионной точности. Тем не менее, при задании значений параметров генерирующего оборудования достаточной является точность до 3 значащих знаков после запятой. Именно с такой точностью указываются значения сопротивлений и постоянных времени в справочной литературе и данных собственников генерирующего оборудования. Результат выполнения команды «calibration» при активном состоянии всех представленных выше настраиваемых параметров изображен на рисунке 7.
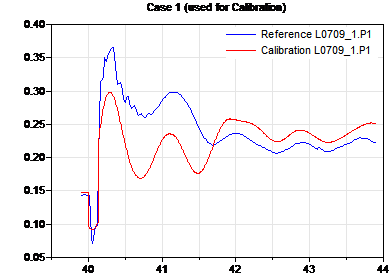
Рис. 7. Активная мощность L0709_1 по данным СМПР и в ПК Dymola в результате выполнения команды «calibration»
Критерием калибровки модели выступает параметр «error» (далее в работе будет обозначено как e0), который представляет собой целевую функцию – сумму квадратов разности между двумя значениями мощности:
`e_(0)=sum_(i=1)^n (y_(i) -y'_(i))^(2)` (3)
где y соответствует выходным данным модели, а y' – эталонным данным. Обычно данный показатель обозначается как SSE (sum of squared errors – сумма квадратов отклонений) и используется в статистике. При делении данного показателя на общее число измерений может быть получен другой широко используемый в статистике показатель – MSE (mean squared error), при дополнительном вычислении его квадратного корня – RMSE (root mean square error). Процесс минимизации целевой функции основан на алгоритме Левенберга – Марквардта, который представляет из себя доработанный алгоритм Гаусса – Ньютона и используется для решения нелинейных задач наименьших квадратов.
В ходе калибровки значения настраиваемых параметров изменяются таким образом, чтобы минимизировать величину e0. В ходе данной калибровки величина уменьшилась с 0,668808 до 0,429361 о. е. График итерационного изменения e0 представлен на рисунке 8.
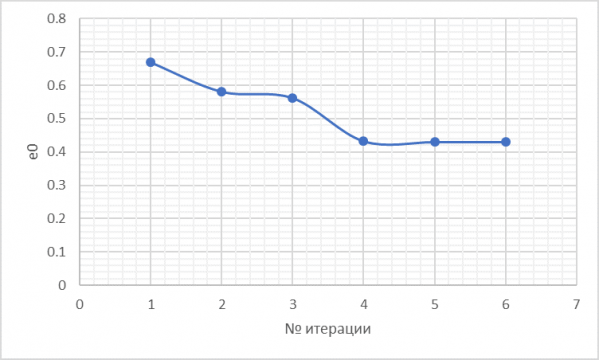
Рис. 8. Изменение параметра e0 во время калибровки
Из таблицы 1 видны текущие проблемы функции калибровки: абсолютно все параметры либо изменяются на бесконечно малую величину, либо не изменяются вовсе. Предположительно, это происходит из-за того, что заложенный разработчиками в функцию «calibration» алгоритм «перегружается» из-за слишком большого числа переменных. В связи с этим предлагается предварительно провести анализ чувствительности параметров, который выполняется вызовом функции «Check calibration sensitivity». Анализ чувствительности позволит определить, какие переменные в наибольшей степени влияют на переходный процесс. После отказа от наименее значимых настраиваемых параметров процесс калибровки должен нормализоваться.
Результатом проверки чувствительности для описанных выше 40 настраиваемых параметров стало сообщение в командной строке программы: «The calibration criteria are insensitive for small variations around the nominal values in the following linear parameter combinations (Критерий калибровки нечувствителен для небольших колебаний вокруг номинальных значений при следующих линейных комбинациях параметров»). Далее представлено 24 линейных комбинации описанных выше настраиваемых параметров. Приведем первую из них:
-G01.K1if - 0,0041*G07.Rf - 0,0021*G07.Tj + 0,0006*G01.K0u + 15,9683*G01.X1d - 0,0492*G01.Rf + 0,5076*G01.X2d - 4,9596*G01.R1q + 0,0028*G01.Tj + 13,9149*G01.Xs
В соответствии с руководством пользователя ПК Dymola, при сохранении постоянным данного соотношения и поочередном изменении настраиваемых параметров величина error не изменяется. Это означает, что необходимо изменять не каждый параметр в отдельности друг от друга, а совокупность представленных в уравнении параметров.
В условиях рассматриваемой задачи представляется достаточно сложным сохранение соотношения между таким большим количеством переменных, в связи с чем данные уравнения допустимо использовать для анализа степени влияния каждого параметра на переходный процесс: чем больше величина множителя перед настраиваемым параметром, тем влияние меньше, и наоборот. Таким образом было выбрано несколько наиболее значимых настраиваемых параметров G01 и G07, к которым относятся K0u, K1if, Tj, X1d, X2d, Rf, R1d, R1q.
Несмотря на уменьшение числа активных настраиваемых параметров примерно в 3 раза, проблема незначительного изменения части параметров осталась актуальной. В связи с этим было принято решение последовательной калибровки модели при активном состоянии только одного настраиваемого параметра либо малых (не более 5 параметров) групп настраиваемых параметров. После завершения калибровки предлагаемое значение настраиваемого параметра или нескольких настраиваемых параметров записываются как начальные условия, и затем калибровка продолжается для другого настраиваемого параметра или группы.
В итоге удалось добиться существенного улучшения степени соответствия кривых активной мощности, полученных в ПК Dymola и по данным СМПР, что представлено на рисунке 9.
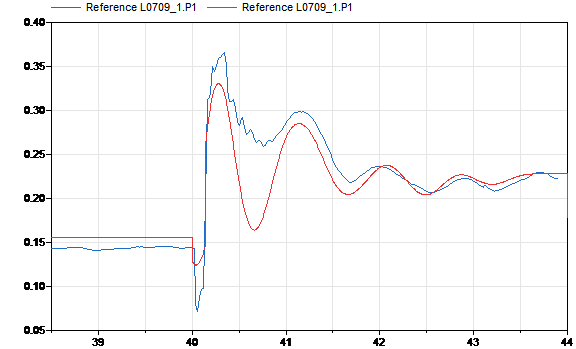
Рис. 9. Активная мощность L0709_1 по данным СМПР (синий цвет) и в ПК Dymola (красный цвет) в результате выполнения команды «calibration»
Величина «error» в диапазоне от 39,9 до 43,9 с составила 0,232332, что почти в 3 раза меньше аналогичной величины для кривых, представленных на рисунке 6.
Сравнительные таблицы с указанием степени изменения наиболее значимых параметров генераторов G01 и G07 приведены ниже.
Таблица 2
Сравнение значений параметров G07 до и после процесса калибровки в ПК Dymola
| Параметр | G07.Kemin | G07.Rf | G07.R1d | G07.R1q | G07.Tj |
| Исходное значение | -0,600 | 0,000601 | 0,000226 | 0,000240 | 19,712 |
| Итоговое значение | -1,000 | 0,000534 | 0,000294 | 0,000168 | 22,770 |
| Отличие, % | 66,670 | 11,150 | 30,090 | 30,000 | 15,510 |
Таблица 3
Сравнение значений параметров G01 до и после процесса калибровки в ПК Dymola
| Параметр | G01.xd | G01.K0u | G01.Xs | G01.X1d | G01.X2d |
| Исходное значение | 0,04100 | 25,000 | 0,00360 | 0,00550 | 0,00390 |
| Итоговое значение | 0,0403 | -10,000 | 0,00340 | 0.00556 | 0,00399 |
| Отличие, % | 1,800 | 140,000 | 5,640 | 1,030 | 2,310 |
| Параметр | G01.X2q | G01.Rf | G01.R1d | G01.R1q | G01.Tj |
| Исходное значение | 0,00390 | 0,000601 | 0,000226 | 0,000240 | 378.880 |
| Итоговое значение | 0,00397 | 0,000781 | 0,000158 | 0,000168 | 5,570 |
| Отличие, % | 1,870 | 30,000 | 30,000 | 30,000 | 6702,150 |
Метод калибровки модели может применяться для учета влияния достаточно большого количества параметров модели и позволяет количественно оценить степень соответствия двух кривых переходного процесса за счет сравнения значений целевой функции на разных этапах расчета.
Применение последнего метода открывает перспективы к практически полной автоматизации процесса валидации динамических моделей энергосистем, что способствует, с одной стороны, созданию и поддержанию в актуальном состоянии максимально достоверных динамических моделей, а с другой стороны, позволит существенно сократить время самого процесса валидации. Тем не менее, для достижения описанной цели требуется создание более совершенного алгоритма калибровки с возможностью более широкого изменения его настроек пользователем. В данном качестве, в частности, могут применяться генетические алгоритмы (далее ГА), применение которых для валидации динамической модели, в частности, описано в работе Мигеля Рубио и других исследователей [Rubio: 6]. Авторы этой работы рассматривают применение специальной библиотеки «GAPILib» для калибровки динамических моделей, реализованных на языке Modelica, на примере изменения параметров модели топливного элемента.
Несмотря на обширные возможности пользователя по изменению параметров ГА, доступных в библиотеке «GAPILib», минусом данного алгоритма калибровки является неприемлемо высокая длительность расчета в программной среде, на что обращают внимание исследователи из Уханьского технологического университета Же Тан и Бо Лиу [Tan: 7], предлагая алгоритм ранней остановки итерационного процесса при достижении заданной величины изменения целевой функции, что предотвращает переобучение системы. Таким образом, ГА могут стать действенным инструментом для валидации ДРМ, однако их внедрение в этот процесс является темой отдельного научного исследования.
* * * * *
В результате аналитической оценки влияния параметров динамической модели на электромеханические переходные процессы удалось добиться соответствия некоторых характеристик полученных в динамической модели кривых данным РАС, а именно:
– изменение частоты колебаний активной мощности в результате изменения инерционной механической постоянной генерирующего агрегата;
– изменение амплитуды колебаний напряжения прямой последовательности в результате изменения напряжения ввода форсировки возбуждения генератора.
В результате попарного изменения коэффициентов регулирования по отклонению и производной отклонения частоты АРВ генератора удалось увеличить степень совпадения частоты и амплитуды колебаний активной мощности, полученных в динамической модели и по данным СМПР. Попарное изменение активной и реактивной проводимости шунта КЗ позволило добиться соответствия величины провала напряжения в результате КЗ.
Наконец, использование функции калибровки позволило значительно увеличить соответствие кривых активной мощности данным СМПР, а также численно оценить степень совпадения двух кривых. В результате варьирования 42 параметров динамической модели величина ошибки соответствия кривых снизилась с 0,668808 до 0,232332 о. е., то есть примерно в 3 раза.
Таким образом, в данной работе были рассмотрены различные способы валидации на примере модели, реализованной с помощью языка Modelica. Результаты валидации для каждого случая демонстрируются как визуально (для всех трех методов), так и численно (для второго и третьего методов).
Примечания
1. Информация взята из инструкции: Dymola: Full User Manual. Lund: Dynamic Modeling Laboratory, 2023. P. 1101.
2. Ibidem, p. 1137.
3. Ibidem, p. 1137-1159.
Список использованных сокращений
АРВ – автоматический регулятор возбуждения;
ВЛ – воздушная линия;
ГА – генетический алгоритм;
ДРМ – динамическая расчетная модель;
КЗ – короткое замыкание;
ОЭС – объединенная энергосистема;
ПК – программный комплекс;
РДУ – региональное диспетчерское управление;
РАС – регистратор аварийных событий;
СМ – синхронная машина;
СМПР – система мониторинга переходных режимов;
ШБМ – шины бесконечной мощности;
ЭЭС – электроэнергетическая система.
Список литературы
Беляев А.Н. Программирование на примере электротехнических и электроэнергетических задач / А.Н. Беляев, С.В. Смоловик. Санкт-Петербург: Нестор, 2006. 120 с.
Смирнов А.Н. Валидация цифровых динамических моделей крупных энергообъединений по данным СМПР: дис. канд. техн. наук: 05.14.02. Санкт-Петербург, 2013. 202 с.
Andersson S. Model calibration of a vertical wind power plant using Dymola/Modelica: Master’s thesis / S. Andersson, J. Strömner. Lund University, 2013. 110 p.
Dorling R. Model validation and the Modelica language // Proceedings of the 4th International Modelica Conference (Hamburg, Germany, March 7-8, 2005). Modelica Association, 2005. P. 374-381.
Gedda S. Derivative-free parameter optimization of functional mock-up units / S. Gedda, C. Andersson, et al. // Proceedings of the 9th International Modelica Conference (Munich, Germany, September 3–5, 2012). Modelica Association and Linköping University Electronic Press, 2012. P. 819-828. DOI: 10.3384/ecp12076819
Rubio М.А. GAPILib – a Modelica library for model parameter identification using genetic algorithms / M.A. Rubio, A. Urquia, et al. // Proceedings of the 4th International Modelica Conference (Vienna, Austria, September 4–5, 2006). Modelica Association, 2006. P. 335-345.
Tan Z. A Calibration method based on heteroscedastic evolutionary Bayesian optimization for simulation system of HVAC / Z. Tan, B. Liu // Proceedings of the 6th International Conference on Robotics, Intelligent Control and Artificial Intelligence (RICAI) (Nanjing, China, December 6–8, 2024). Nanjing, 2024. P. 1035-1039. DOI: 10.1109/RICAI64321.2024.10911783




