1. Введение
В последнее время модели факторизации привлекли большое внимание исследователей в области интеллектуальных информационных систем и машинного обучения. Такие модели продемонстрировали отличные возможности прогнозирования в нескольких важных программах, например, в рекомендательных системах. Эти системы разработаны для того, чтобы предоставлять рекомендации пользователю на основе разнообразных факторов. Они обрабатывают обширный объем сведений, фильтруя наиболее значимую информацию на основе пользовательских входных данных и других факторов, учитывая при этом предпочтения и интересы пользователя. Наиболее хорошо изученной моделью факторизации является матричная факторизация, которая позволяет нам предсказать связь между двумя категориальными переменными. Факторизационные машины являются в некотором смысле обобщением матричной факторизации. Основное достоинство данной модели состоит в том, что она обладает хорошей способностью к обучению на разреженных данных и позволяет строить рекомендательные системы на основе большого количества категориальных и вещественных признаков. Постоянные исследования в данной области продолжают расширять сферу применения факторизационных машин, делая их все более эффективными и способными адаптироваться к различным задачам, что, в свою очередь, способствует развитию и совершенствованию рекомендательных систем.
Рассмотрим линейную модель с учетом взаимодействия факторов:
`sfy(sfx;bbTheta)= sfw_(0) + sum_(j=1)^p sfw_(j)x_(j) + sum_(i=1)^psum_(j=i+1)^psfw_(ij)x_(i)x_(j).` (1)
В данном случае возникает проблема, так как число параметров представленной модели квадратично зависит от числа признаков: `(p-1)//2+p+1`. Если среди признаков есть категориальные переменные с большим числом категорий, то после бинарного кодирования число параметров значительно увеличится. В статье [Rendle, 2010] было предложено решение этой проблемы. Предположим, что вес взаимодействия определяется низкоразмерными векторами `sfv_(i),sfv_(j)inRR^(k) ` через их скалярное произведение:
`sfy(sfx;bbTheta)= sfw_(0) + sum_(j=1)^p sfw_(j)x_(j) + sum_(i=1)^psum_(j=i+1)^p(sfv_(i),sfv_(j))x_(i)x_(j).` (2)
В этом случае число параметров линейно зависит от числа признаков: `pk+p+1`.
Современные рекомендательные системы часто используют сложные модели машинного обучения. Эти модели обычно включают большое количество параметров и несколько параметров регуляризации, чтобы предотвратить переобучение. Для факторизационных машин было предложено несколько методов обучения. В зависимости от значений, которые могут принимать наблюдения, различают задачу регрессии и задачу классификации. В исходной статье 2010 года [Rendle, 2010] для факторизационных машин был предложен метод стохастического градиентного спуска (SGD), который можно использовать как для задачи регрессии, так и для задачи классификации. Кроме того, для задачи регрессии в [Rendle, 2011] авторы предложили использовать метод чередующихся наименьших квадратов (ALS). И в 2011 году были предложены байесовские факторизационные машины [Freudenthaler]. В рамках иерархической байесовской модели авторы предложили использовать Методы Монте-Карло по схеме марковских цепей (MCMC – Markov Chain Monte Carlo), а точнее cхему Гиббса. При этом ранее методы Монте-Карло рассматривались только для задачи регрессии и задачи бинарной классификации с пробит-функцией связи. На основании проведенных экспериментов в [Freudenthaler], было обнаружено, что MCMC продемонстрировали более высокое качество прогнозирования по сравнению с другими методами. Превосходство заключается в том, что Методы Монте-Карло по схеме марковских цепей учитывают неопределенность параметров модели, что обеспечивает точные прогнозы даже для моделей с большим количеством категориальных и вещественных признаков. Также использование байесовского подхода естественным образом включает регуляризацию через априорное распределение параметров, что помогает избежать переобучения модели.
Анализируя литературу и документацию к различным библиотекам для факторизационных машин, мы выяснили, что для факторизационных машин с логистической функцией активации был предложен только метод стохастического градиентного спуска. Поэтому в работе была сделана попытка разработать схему Гиббса для логистической функции связи.
Структура статьи организована следующим образом: в разделе 2 приводится описание байесовских факторизационных машин. Подробное описание применения схемы Гиббса для байесовских факторизационных машин представлено в разделе 3. Раздел 4 посвящен результатам, полученным в ходе численных экспериментов, проведенных как на синтетических, так и на реальных данных, с целью продемонстрировать эффективность предложенного метода. В заключительном разделе 5 представлены выводы, основанные на полученных результатах, и рассматриваются дальнейшие планы и направления исследований в контексте проделанной работы.
2. Байесовские факторизационные машины
Байесовский подход в машинном обучении состоит в задании априорных распределений на оцениваемые параметры. При этом на практике часто используют так называемые байесовские иерархические модели, когда для параметров априорных распределений (которые будем называть гиперпараметрами) также задаются свои априорные распределения. В настоящей работе рассматривается байесовская модель, предложенная в работе [Freudenthaler]. Кратко опишем структуру данной модели, для чего выделим три множества параметров:
- Исходные параметры `bbTheta = {sfw_(0),sfw_(j),v_(j,s), j = 1,...,p,s=1,...,k}`;
- Параметры априорных распределений (гиперпараметры) `bbTheta_(H) = {mu_(sfw),lambda_(sfw),mu_(v_(s)),lambda_(v_(s)),s=1,...,k}`;
- Фиксированные параметры априорных распределений для гиперпараметров `bbTheta_(0) = {mu_(0), mu_(sfw_0),lambda_(sfw_0), gamma_(0), alpha_(lambda), beta_(lambda)}`.
Пусть имеется обучающая выборка `{x_i,y_i}`, `i = bar(1,n)`, где `x_(i)inRR^(p), y_(i)in{0,1}`. Статистическая модель для факторизационных машин имеет следующий вид:
`y_i` ~ `Ber(p_i)`, `i=1,...,n`
` p_i = F(sfy(sfx_i,bbTheta))`, `i=1,...,n `` `
` F(x) = 1//(1+e^(-x)). `
` `Рассматриваемая байесовская иерархическая модель может быть задана в виде графовой модели, представленной на рис. 1.
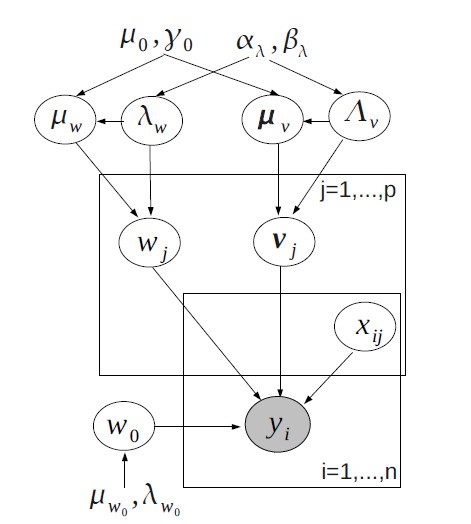
Рис. 1. Иерархическая байесовская модель [Freudenthaler]
Для всех параметров из множеств `bbTheta`и `bbTheta_H` задаются следующие априорные распределения:
`sfw_0` ~ `sfN(mu_(sfw_(0)), lambda_(sfw_(0)))`,
`sfw_j` ~ `sfN(mu_(sfw), lambda_(sfw))`, `j=bar(1,p)`,
`v_(j,s)` ~ `sfN(mu_(v_(s)), lambda_(v_(s)))`, `j=bar(1,p)`, `s=bar(1,k)`,
`mu_(sfw)` ~ `sfN(mu_(0), gamma_0lambda_(sfw))`,
`mu_(v_s)`~ `sfN(mu_(0), gamma_0lambda_(v_s))`, `s=bar(1,k)`,
`lambda_sfw` ~ `Ga(alpha_lambda, beta_lambda)`,
`lambda_(v_s) ` ~ `Ga(alpha_lambda, beta_lambda) `, `s=bar(1,k).`
Здесь `sfN(mu, lambda)` означает нормальное распределение с математическим ожиданием `mu` и дисперсией `1//lambda`; `Ga(alpha,beta)` – гамма-распределение с параметром формы `alpha` и параметром масштаба `beta`.
3. Схема Гиббса для байесовских факторизационных машин
Для нахождения оценок в сложных байесовских моделях применяются методы приближенного байесовского вывода, в том числе на основе методов Монте-Карло по схеме марковских цепей.
Метод Н. Полсона, Дж. Скота и Дж. Уиндла был предложен в статье 2013 года [Polson] для логистической регрессии, но с некоторыми изменениями его можно адаптировать для модели факторизационных машин. В соответствии с подходом задается случайный вектор `bbomega = (omega_1,...,omega_n)^ttT` так, что `omega_i` имеет распределение Пойа-Гамма:
`omega_i` ~ `PG(1,sfy(sfx_i,bbTheta))` , ` i=bar(1,n)`. (3)
Для многомерной случайной величины `(bbomega, bbTheta, bbTheta_H)`применяется схема Гиббса (Gibbs sampling). Для этого требуется, чтобы была возможность генерировать реализации из условных распределений `bbomega|bbTheta,bbTheta_H`, `bbTheta|bbomega,bbTheta_H` , `bbTheta_H|bbomega, bbTheta`. Исходя из предположений о графовой модели, получаем такое совместное распределение модели:
`p(bbTheta, bbTheta_H, bbomega, sfy|bbX, bbTheta_0) prop p(bbomega, sfy|bbTheta, bbX)p(bbTheta|bbTheta_H, bbTheta_0)p(bbTheta_H|bbTheta_0) `
`propprod_(i=1)^n p(bbomega_i,y_i|bbTheta,bbX)prod_(thetainbbTheta)p(theta|bbTheta_H,bbTheta_0)prod_(theta_(h)inbbTheta_H)p(theta_h|bbTheta_0)` , (4)
где `sfy` - вектор откликов, `bbX={x_i^ttT}` – матрица признаков.
Для применения схемы Гиббса из совместного распределения модели находятся полные условные распределения для всех `thetainbbTheta` и `theta_hinbbTheta_H` :
`p(theta|bbTheta\\{theta},bbTheta_H)`, (5)
`p(theta_h|bbTheta_H\\{theta_h},bbTheta).` (6)
Для гиперпараметров получаем следующие распределения:
`p(lambda_h|bbTheta_H\\{lambda_h}, bbTheta, bbTheta_0) = Ga(lambda_h|bar(alpha)_h, beta_h)`, (7)
`p(mu_h|bbTheta_H\\{mu_h}, bbTheta, bbTheta_0) = sfN(mu_h|bar(mu)_h, bar(sigma)_h^2)`, (8)
где `hin{sfw,v_1,...,v_k}`, `bar(alpha)_h`,`bar(beta)_h`, `bar(mu)_h`, `bar(sigma)_h^2` зависят от остальных значений параметров. Здесь `Ga(*|alpha,beta)` – плотность гамма-распределения с параметром формы `alpha` и параметром масштаба `beta`, а `sfN(*|mu,sigma^2)` – плотность нормального распределения с математическим ожиданием `mu ` и дисперсией `sigma^2` .
Полные условные распределения для каждого исходного параметра:
`p(theta|bbTheta\\{theta},bbTheta_H, bbTheta_0, bbomega, sfy, bbX) = sfN(theta|bar(mu)_theta, bar(sigma)_theta^2)`, (9)
где `bar(mu)_theta` , `bar(sigma)_theta^2` , зависят от значений остальных параметров, обучающей выборки и вектора `bbomega`. Прямой расчет `bar(mu)_theta`, `bar(sigma)_theta^2` требует `O(npk)`операций (для каждого элемента обучающей выборки `O(pk)` операций). Принимая во внимание свойство полилинейности модели
`sfy(sfx,bbTheta) = g_theta(sfx)+thetah_theta(sfx)`, `AA theta in bbTheta`, (10)
можно сократить число операций до `O(n)` , следуя подходу, предложенному ранее в статье [Rendle 2011], с незначительными изменениями.
4. Результаты
Численные эксперименты проводились как на синтетических, так и на реальных данных. В частности, в серии M экспериментов для синтетических данных рассчитывалась оценка исходных параметров модели помощью схемы Гиббса на основе распределения Пойа-Гамма и находилось эмпирическое распределение для показателя AUC (площадь под ROC-кривой).
Данный показатель был рассчитан для метода стохастического градиентного спуска и для реализованной схемы Гиббса, при этом рассматривается ситуация, когда гиперпараметры `Theta_H` фиксированы (Рис. 2.).
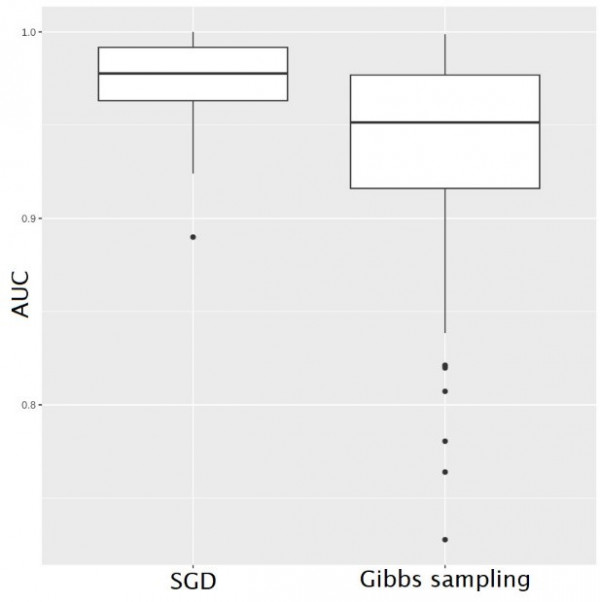
Рис. 2. SGD vs. Gibbs sampling
Исходя из диаграммы, видно, что значения для двух разных методов близки между собой и лежат в диапазоне от 0.9 до 1. Кроме того, эксперименты были проведены на реальных данных, в частности, показатели AUC были подсчитаны для стандартных наборов данных (Pima и т.д.) [Chopin].
Таблица
Показатели AUC для стандартных наборов данных
| Dataset | AUC Gibbs sampling | AUC SGD |
| Pima (Indian diabetes) | 0.776 | 0.617 |
| Sonar | 0.814 | 0.885 |
| Banknote | 0.92 | 0.85 |
| Australian Credit Approval | 0.943 | 0.691 |
| Musk (Version 2) | 0.97 | 0.715 |
Из таблицы видно, что только в случае набора данных Sonar показатель AUC для схемы Гиббса ниже, чем для AUC SGD, что, вероятнее всего, связано с небольшим количеством переменных в представленном наборе данных.
5. Заключение
В результате работы был реализован новый подход для обучения байесовских факторизационных машин с логистической функцией активации на основе специального варианта схемы Гиббса с дополнительными переменными, имеющими распределение Пойа-Гамма. Проведены вычислительные эксперименты на синтетических и на реальных данных, иллюстрирующие качество предложенного подхода. В дальнейшем предполагается провести сравнительный анализ различных методов обучения факторизационных машин, что поможет выявить преимущества и недостатки каждого метода и определить наиболее эффективные методы обучения и применения факторизационных моделей в различных прикладных задачах. Кроме того, планируется провести дополнительные эксперименты, включая апробацию алгоритма на более крупных наборах данных, содержащих большое количество категориальных признаков, исследовать различные расширения и обобщения методов факторизации для задач многоклассовой классификации, учета пропущенных значений, скрытых факторов и т. п.
Список литературы
Chopin N. Leave Pima Indians Alone: Binary Regression as a Benchmark for Bayesian Computation / N. Chopin, J. Ridgway. Statist. Sci. 32 (1) 64–87, 2017. DOI: 10.1214/16-STS581
Freudenthaler C. Bayesian Factorization Machines / C. Freudenthaler, L. Schmidt-Thieme, S. Rendle // Proceedings of the NIPS Workshop on Sparse Representation and Low-rank Approximation 995-1000, 2011.
Polson N.G. Bayesian Inference for Logistic Models Using Polya–Gamma Latent Variables / Nicholas G. Polson, James G. Scott & Jesse Windle // Journal of the American Statistical Association. 2013.
Rendle S. Factorization machines // Proceedings of the 10th IEEE International Conference on Data Mining. IEEE Computer Society, 2010.
Rendle S. Fast context-aware recommendations with factorization machines // S. Rendle, C. Freudenthaler, Z. Gantner, L. Schmidt-Thieme // Proceedings of the 34th ACM SIGIR Conference on Reasearch and Development in Information Retrieval, 2011.




