Ежегодно на платформе IQ.KARELIA1 проходят тестирования по различным дисциплинам сотни студентов [Мощевикин]. Тест «Недесятичная арифметика» предлагается студентам первого и третьего курсов направлений «Информатика и вычислительная техника» и «Приборостроение». Стоит отметить, что вступительные испытания в магистратуру ФТИ ПетрГУ также проводятся на платформе IQ.KARELIA [Балашов].
Тесты на платформе IQ.KARELIA имеют два режима: обычное тестирование и контрольное тестирование. Для теста «Недесятичная арифметика» обычное тестирование состоит из вопросов открытой базы и направлено на наработку навыка студента работать с различными системами счисления, а также производить различные математические и булевые операции в них. Контрольное тестирование предназначено для оценки навыков и знаний студента [Соловьев], оно включает в себя вопросы из открытой и закрытой баз. Прохождение теста считается успешным, если при ответе на 11 вопросов теста студент набрал суммарно как минимум 4.5 балла из 5 и при этом уложился в отведенное время 14 минут.
Общее количество вопросов в тесте «Недесятичная арифметика», разбитых на категории, а также количество ответов на эти вопросы при прохождении тестирования и накопленных для последующего анализа, приведено в таблице 1.
Цель исследования – проверка корректности алгоритма выдачи вопросов и выявление нерепрезентативных или некорректных вопросов. В задачи исследования входят проверка алгоритма выдачи вопросов на равномерность и соответствие текущему уровню сложности, а также анализ результатов тестирований студентов с выявлением наиболее сложных тем.
Таблица 1
Общая статистика по тестированиям
| Количество вопросов в тесте «Недесятичная арифметика» | Количество ответов на вопросы | |||
| Сложность вопросов | Открытые | Закрытые | Обычное | Контрольное |
| Простые | 30 | 44 | 32 тыс. | 2.1 тыс. |
| Нормальные | 82 | 137 | 88.3 тыс. | 6.6 тыс. |
| Сложные | 14 | 18 | 14.9 тыс. | 0.8 тыс. |
Основные методы исследования:
- Использование инструментов Python. Для обработки и анализа данных применялись библиотеки Python, такие как Pandas [Абдрахманов] (для работы с табличными данными), Scipy (для статистического анализа) и Matplotlib (для визуализации). Эти инструменты обеспечили эффективную обработку больших объёмов данных и точность результатов.
- Статистический анализ данных. Для проверки равномерности распределения вопросов в тесте использовался критерий согласия Хи-квадрат [Ивченко: 109-114]. Этот метод позволил сравнить наблюдаемые частоты выдачи вопросов с теоретически ожидаемыми при равномерном распределении. Также был рассчитан p-уровень значимости (p-value) для подтверждения или опровержения гипотезы о равномерности.
- Анализ процента правильных ответов. Для оценки корректности вопросов и их соответствия уровню сложности был проведён анализ процента правильных ответов на каждый вопрос. Это позволило выявить вопросы, которые могут быть перенесены в другую категорию сложности, а также исключить некорректно составленные вопросы.
- Визуализация данных. Для наглядного представления результатов исследования использовались графики и диаграммы, построенные с помощью библиотеки Matplotlib. Визуализация включала гистограммы распределения вопросов, графики зависимости времени прохождения теста от номера попытки и распределение процента правильных ответов по уровням сложности.
- Группировка и анализ по тематикам. Вопросы были сгруппированы по тематикам, после чего для каждой темы был рассчитан средний процент правильных ответов. Это позволило выявить проблемные темы, которые вызывают наибольшие трудности у студентов.
- Анализ динамики навыков студентов. Для оценки улучшения навыков студентов анализировалось время прохождения теста в зависимости от номера попытки. Это позволило подтвердить, что студенты действительно развивают навыки арифметического счёта в различных системах счисления, а не просто заучивают ответы.
Со слов студентов, при прохождении теста у них создавалось впечатление неравномерности выдачи вопросов: им казалось, что одни вопросы выдаются чаще, чем другие. Для проверки того, что алгоритм генерации вопросов в тесте действительно распределяет вопросы равномерно, была построена гистограмма распределения, представленная на рисунке 1. В качестве исходных данных для нее были взяты только результаты контрольного тестирования, так как в нём используются вопросы из обеих баз: открытой и закрытой.
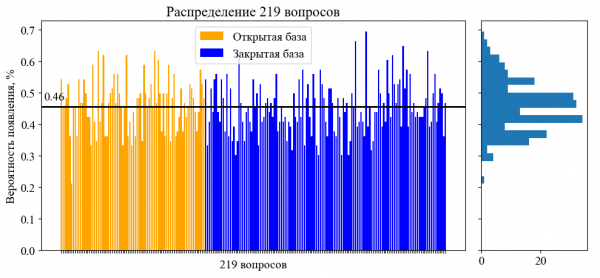
Рис. 1. Графики распределения 219 вопросов из тестирования «Недесятичная арифметика»
Вероятность выдачи каждого из 219 вопросов при равномерном распределении равняется 1/219 = ~0.46 %. На гистограмме (рисунок 1 слева) черной сплошной линией показана средняя вероятность выдачи вопроса по выборке, которая составила ту же величину ~0.46 %. На рисунке 1 справа отображено распределение вероятности появления (ось y) и частота выдачи вопросов для данной вероятности (ось x). Распределение на рисунке 1 справа показывает, что наиболее часто встречаются вопросы с вероятностью появления близкой к 0.46 (отмеченной на графике черной линией). Распределение, представленное на рисунке 1 справа, визуально напоминает равномерное, однако имеются выбросы вероятности появления вопроса как в большую, так и в меньшую сторону. Данные выбросы могут быть вызваны недостаточно большим размером выборки. Для проверки распределения следует предложить гипотезу о равномерности распределения вопросов.
Доказательством того, что выдача вопросов не противоречит равномерной, служит критерий согласия Хи-квадрат и соответствующий p-уровень значимости (p-value). Критерий Хи-квадрат используется для сравнения наблюдаемых и ожидаемых частот, позволяя оценить, насколько близко реальное распределение соответствует теоретическому. В данном исследовании были проанализированы два массива данных: вероятности, полученные на основе реальной выборки (см. рисунок 1, справа), и вероятности для идеальной выборки, которая подчиняется равномерному распределению.
Для проверки гипотезы был рассчитан p-уровень значимости, который составил 0.502. Согласно правилам статистики, если p-value превышает пороговое значение (в исследовании пороговое значение выбрано 0.05), у нас недостаточно оснований для отклонения нулевой гипотезы. Это означает, что наблюдаемые данные не противоречат предположению о равномерном распределении вопросов. Однако важно отметить, что высокий p-value не доказывает, что распределение действительно равномерное, а лишь указывает на отсутствие статистически значимых отклонений от него.
Для ответа на вопрос, действительно ли студенты вырабатывают навык, а не заучивают ответы, построен график зависимости времени прохождения тестирования от номера попытки студента, представленный на рисунке 2. Под навыком понимается умение студентов правильно и быстро проводить арифметические операции в различных системах счисления.
Для анализа улучшения навыков студентов были отобраны результаты тестирований с набранным баллом выше 3.2. Данные были обработаны с использованием метода скользящего окна: каждая корзина включала две ближайшие попытки (например, попытки 1 и 2, 3 и 4 и т. д.). Фактически, мы применяли скользящее окно размером в две точки, где каждая пара попыток усреднялась. Например, для студента с 80 попытками было создано 40 корзин, каждая из которых содержала усреднённые значения времени для двух последовательных попыток. Результат представлен в виде тёмно-синих точек на рисунке 2 (обычное среднее).
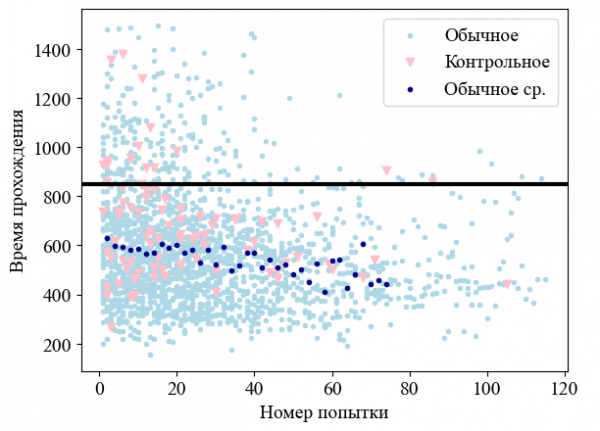
Рис. 2. Зависимость времени прохождения тестирования от номера попытки студента
Анализ показал, что с увеличением числа попыток среднее время прохождения обычного тестирования уменьшилось с ~10.4 минут до ~7.3 минут. Это свидетельствует о том, что студенты действительно нарабатывают навык арифметического счёта в различных системах счисления. При этом среднее время прохождения контрольного тестирования оставалось стабильным и составляло ~10.7 минут, что может быть связано с более высокой сложностью вопросов в этом режиме. Также стоит отметить, что с увеличением числа попыток уменьшается количество результатов, время которых превышает допустимое время для контрольного тестирования (14 минут – чёрная горизонтальная линия на рисунке 2). Интересно, что три студента совершили более 80 попыток, но только двое из них дошли до контрольного тестирования, при этом ни один из них не набрал необходимый балл.
Для выявления вопросов, не соответствующих их текущему уровню сложности, построено распределение доли вопросов для определенного процента правильных ответов для вопросов с различным уровнем сложности (рисунок 3).
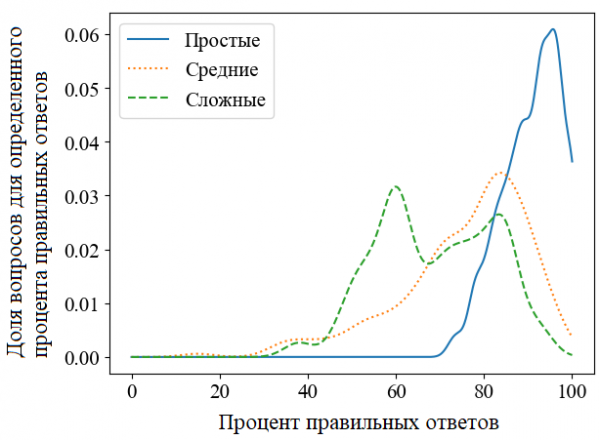
Рис. 3. Распределение доли вопросов для определенного процента правильных ответов для вопросов различного уровня сложности
Данный график (рисунок 3) показывает, что, например, самый частый процент правильных ответов в простых это ~96 %. Для средних самый частый процент правильных ответов равен ~83 %. В целом, на простые вопросы отвечают более правильно, чем на средние и сложные. Однако для сложных вопросов следует отметить бимодальность распределения (рисунок 3, сложные). Правая мода штриховой кривой полностью находится под кривой вопросов средней сложности. Очевидно, что сложные вопросы с процентом правильных ответов выше 60 % следует перенести в категорию средних и легких вопросов. Вопросы среднего уровня сложности, имеющие процент правильных ответов более 80 %, стоит отнести к простому уровню.
Отсутствие вопросов с процентом правильных ответов, близким к нулю, свидетельствует о том, что в тесте «Недесятичная арифметика» отсутствуют некорректно составленные вопросы. При этом необходимо отметить, что в системе IQ.KARELIA после прохождения теста 10 раз у студентов есть возможность получить показатели успешности освоения по всем темам в тесте.
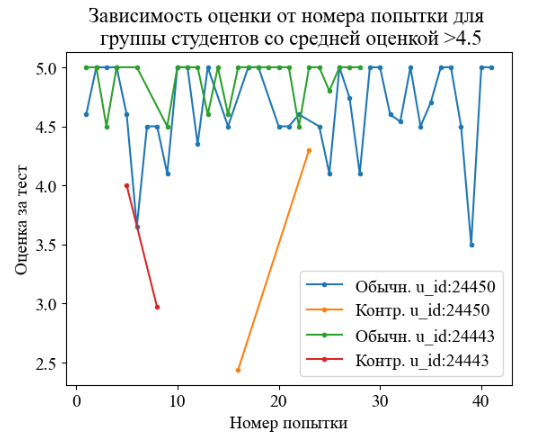
Рис. 4. Зависимость оценки от номера попытки для группы студентов со средней оценкой более 4.5.
На данном графике представлена динамика прохождения теста двумя студентами. Для приватности ФИО студентов заменены на u_id (user_id). Основная часть оценок прижата к верхнему краю, то есть к оценке = 5, но при этом имеются выбросы в сторону оценки = 2.5. Данные выбросы являются результатами контрольного тестирования, на котором студенты, заучившие ответы, встретили неизвестные вопросы или новые задачи.
Исходя из вышесказанного можно сделать вывод, что студенты даже после неудачи (первый результат Контр. u_id:24443) больше надеются на то, что в следующий раз попадутся вопросы полегче, а не пытаются изучить проблемный материал.
Для определения проблемных для студентов тем все вопросы были сгруппированы по их тематикам, далее был найден средний процент правильных ответов для каждой темы. Результаты представлены в таблице 2. Видно, что в темах «Арифметика» (69.61 %), «Арифметика усложненная» (61.86 %) и «Операции сдвига влево-вправо» (64.54 %) студенты разбираются хуже, чем в остальных. Поэтому им нужно потратить дополнительное время для улучшения своих показателей в них.
При анализе ответов пользователей выяснилось, что из-за невнимательности студентов оценка за тестирование уменьшается в среднем на 1.2 %. Например, студент указывает 0b при записи 0b0111, или 0x при вводе 0xAE, а в регламенте указано, что префиксы и/или лидирующие нули должны отсутствовать.
Таблица 2
Тематики тестирования и их средние проценты правильных ответов
| Тематика | Средний процент правильных ответов |
| Преобразование из одной системы счисления в другую | 80.92 |
| AND OR NOT | 73.84 |
| Арифметика | 69.61 |
| Арифметика усложненная | 61.86 |
| Операции сдвига влево-вправо | 64.54 |
| Операции XOR | 82.33 |
На основе проведённого анализа были предложены следующие рекомендации:
1. Оптимизация сложности вопросов. Часть вопросов, которые были классифицированы как «сложные», но имеют высокий процент правильных ответов, следует перенести в категорию «нормальные». Это позволит более точно оценивать знания студентов и избежать ситуаций, когда студенты теряют баллы из-за несоответствия сложности вопроса их уровню подготовки.
2. Добавление новых типов заданий. Для повышения интереса студентов и улучшения их навыков рекомендуется добавить в тест задания, требующие не только арифметических вычислений, но и логического мышления. Например, задачи на поиск закономерностей в последовательностях чисел или на анализ алгоритмов.
3. Улучшение обратной связи. После прохождения теста студенты должны получать более детальную информацию о своих ошибках, включая объяснение правильного решения и ссылки на учебные материалы для повторения проблемных тем.
Таким образом, в результате исследования можно сделать следующие выводы.
- Разработанный на языке программирования Python ряд скриптов для обработки данных и анализа тестирования «Недесятичная арифметика» позволяет эффективно собирать, обрабатывать и анализировать результаты тестирований.
- Анализ алгоритма выдачи вопросов показывает, что алгоритм не противоречит предположению о равномерном распределении выдачи вопросов. Наблюдаемые данные о частоте появления вопросов не противоречат равномерному распределению.
- В результате исследований автор пришёл к выводу, что часть вопросов из групп «нормальные» и «сложные» целесообразно перевести в группу «простые». Это вызвано тем, что некоторые вопросы, классифицированные как сложные или нормальные, на практике оказались более легкими для студентов, чем ожидалось.
- Проанализировав результаты тестирований, автор не выявил неверно составленных вопросов в тесте «Недесятичная арифметика», что свидетельствует о высоком уровне проработки тестовых материалов.
- Также был составлен список нерепрезентативных вопросов в тесте «Недесятичная арифметика», которые не дают точной оценки уровня знаний студентов, что требует их пересмотра или улучшения.
- В ходе исследования автором были выявлены проблемные для студентов темы, такие как «Арифметика», «Арифметика усложненная», «Операции сдвига влево-вправо», которые вызывали наибольшие трудности в решении заданий. Средний процент правильных ответов в них составил менее 70 %. Автором были предложены рекомендации по адаптации материалов для лучшего понимания данных тем студентами.
Примечания
1 IQ.KARELIA.RU: Онлайн тестирование по многим предметам: сайт. Url: https://iq.karelia.ru (дата обращения: 7.02.2025).
Список литературы
Абдрахманов М.И. Pandas. Работа с данными. Москва: Devpractice Team, 2020. 171 с.
Балашов Д.И. Использование системы онлайн-тестирования знаний iq.karelia.ru для проведения вступительных испытаний при приеме в магистратуру физико-технического института ПетрГУ / Д.И. Балашов, А.П. Мощевикин, А.В. Соловьев // Цифровые технологии в образовании, науке, обществе: материалы XI(1) Всероссийской научно-практической конференции (Петрозаводск, 27–30 ноября 2017 г.). Петрозаводск, 2017. С. 13-16. Url: https://it2017.petrsu.ru/publications.
Ивченко Г.И. Математическая статистика / Г.И. Ивченко, Ю.И. Медведев. Москва: Высшая школа, 1984. 248 с.
Мощевикин А.П. Система on-line тестирования iq.karelia.ru / А.П. Мощевикин, А.В. Соловьев // IT-инновации в образовании: Материалы Всерос. научно-практ. конф. (Петрозаводск, 27-30 июня 2005 г.). Петрозаводск: ПетрГУ, 2005. С. 171-175.
Соловьев А.В. Использование системы онлайн-тестирования знаний iq.karelia.ru для разработки контрольно-измерительных материалов по различным дисциплинам / А.В. Соловьев, А.П. Мощевикин // Научно-образовательная информационная среда XXI века: материалы IX Всероссийской научно-практической конференции (Петрозаводск, 23–25 сентября 2015 г.). Петрозаводск, 2015. С. 168-171.




